Blog

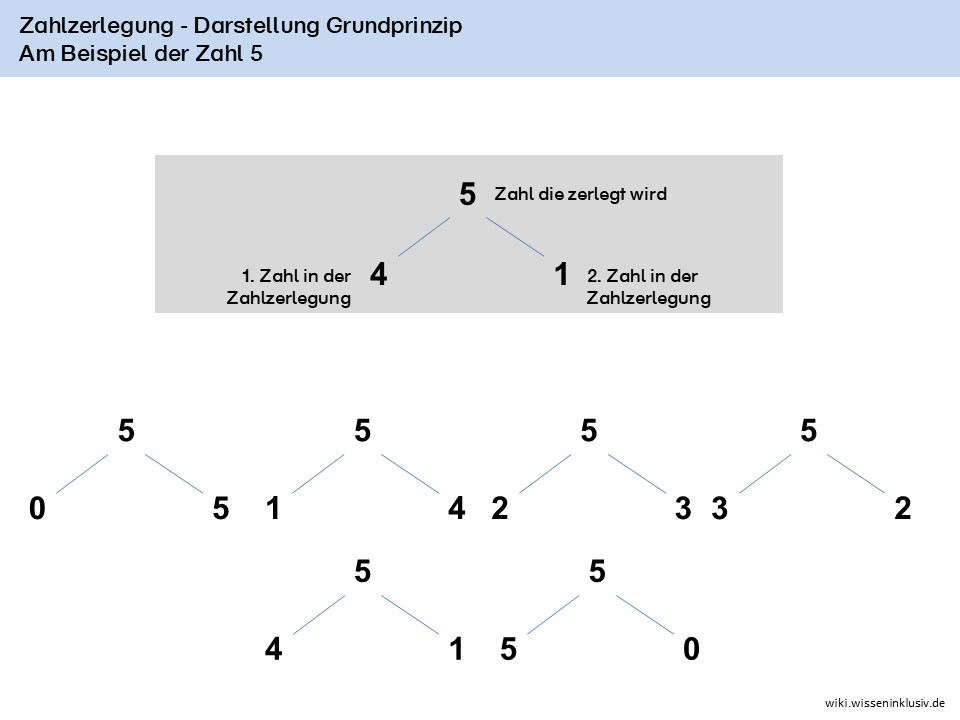
Bei der einfachen Zahlzerlegung im Zahlenraum 10 wird eine Zahl zwischen 1 und 10 in zwei Zahlen zerlegt.

Die Summe dieser beiden Zahlen ergibt immer die Zahl selbst.

Zahlen können auseinander genommen (Zahlzerlegung) und auch wieder zusammengesetzt werden (z. B. durch Addition).

Zahlzerlegung

• Bei der Zahlzerlegung in diesem Zusammenhang ist gemeint, dass eine Zahl in zwei Zahlen zerlegt wird.
• Die Zahlzerlegung besteht hier daher aus zwei Zahlen.
• Mit den zerlegten Zahlen können unterschiedliche Rechenaufgaben absolviert werden.
• Bei Addition steht zwischen den zwei Zahlen, in die eine andere zerlegt wurde, ein +.
• Die zwei Zahlen addiert ergeben die Ergebniszahl (das ist die Zahl, die zerlegt wurde).
• Es gibt so viele Zahlzerlegungen wie die Ergebniszahl Plus 1.
  • Bei der Zahl 1 sind es zwei Zahlzerlegungen.
  • Bei der Zahl 2 sind es drei Zahlzerlegungen.
  • Bei der Zahl 3 sind es vier Zahlzerlegungen.
  • usw.
• Bei geraden Zahlen ist in der Mitte aller Zerlegungen eine Zerlegung mit zwei gleichen Zahlen (=Verdopplung).
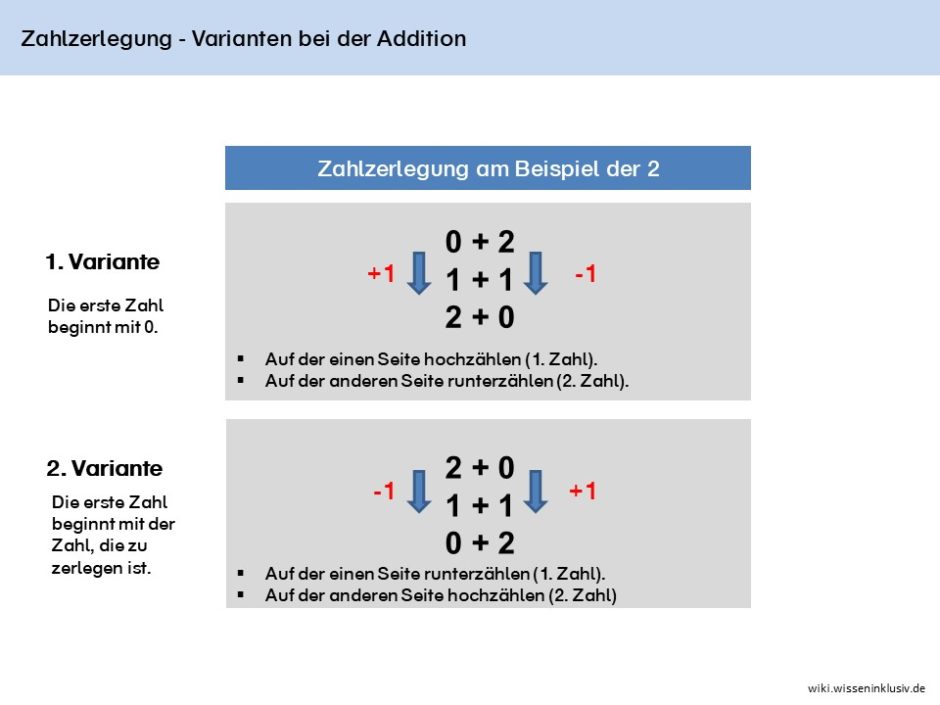
• Je nach gewählter Zahlzerlegungsvariante (siehe weiter unten) nimmt die erste und die zweite Zahl von oben nach unten ab oder zu.

Zahlzerlegung für die Zahlen von 1 bis 3

In welche Zahlen lässt sich die 1 zerlegen?

• 0 + 1
• 1 + 0

Jedes Ergebnis ergibt jeweils 1.

In welche Zahlen lässt sich die 2 zerlegen?

• 2 + 0
• 1 + 1 (bei geraden Zahlen ist in der Mitte aller Zerlegungen eine Zerlegung mit zwei gleichen Zahlen)
• 0 + 2

Jedes Ergebnis ergibt jeweils 2.

In welche Zahlen lässt sich die 3 zerlegen?

• 0 + 3
• 1 + 2
• 2 + 1
• 3 + 0

Jedes Ergebnis ergibt jeweils 3.

Einfache Vorgehensweise bei der Zahlzerlegung

Bei der Zahlzerlegung je Zahl kannst du einem Muster folgen. Dabei kannst du in zwei Varianten vorgehen.

1. Variante am Beispiel der 3 erklärt

• Beginne mit der Zahl selbst, hier der 3. Die zweite Zahl muss eine Null sein, damit die Rechnung 3 ergibt -> 3 + 0
• Ziehe von der ersten Zahl eins ab, du landest bei der 2. Zähle bei der zweiten Zahl eins hoch. Du landest bei der 1 -> 3 + 1
• Ziehe von der nächsten Zahl eins ab, du landest bei 1. Zähle bei der zweiten Zahl eins hoch. Du landest bei der 2 -> 1 + 2
• Ziehe von der nächsten Zahl eins ab, du landest bei der 0. Zähle bei der zweiten zahl eins hoch. Du landest bei der 3 -> 0 + 3

2. Variante am Beispiel der 3 erklärt

• Beginne mit der 0.
• Die erste Zahl in der Rechnung ist die 0, die zweite Zahl ist automatisch die Zahl selbst. Die Zahlenzerlegung lautet 0 + 3
• Zähle die erste Zahl um eins hoch, du landest bei der 1. Ziehe von der zweiten Zahl eins ab. Du landest bei der 2. Die Zahlenzerlegung lautet 1 + 2
• Zähle wieder die erste Zahl um eins hoch, du landest bei der 2. Ziehe von der zweiten Zahl wieder eins ab. Du landest bei der 1. -> Die Zahlenzerlegung lautet 2 + 1
• Zähle wieder die erste Zahl um eins hoch, du landest bei der 3. Ziehe von der zweiten Zahl wieder eins ab. Du landest bei der 0. -> Die Zahlenzerlegung lautet 3 + 0

Zahlzerlegung für die Zahlen 4 bis 10

In welche Zahlen lässt sich die 4 zerlegen?

• 0 + 4
• 1 + 3
• 2 + 2 (bei geraden Zahlen ist in der Mitte aller Zerlegungen eine Zerlegung mit zwei gleichen Zahlen)
• 3 + 1
• 4 + 0

Jedes Ergebnis ergibt jeweils 4.

In welche Zahlen lässt sich die 5 zerlegen?

• 0 + 5
• 1 + 4
• 2 + 3
• 3 + 2
• 4 + 1
• 5 + 0

Jedes Ergebnis ergibt jeweils 5.

In welche Zahlen lässt sich die 6 zerlegen?

• 0 + 6
• 1 + 5
• 2 + 4
• 3 + 3 (bei geraden Zahlen ist in der Mitte aller Zerlegungen eine Zerlegung mit zwei gleichen Zahlen)
• 4 + 2
• 5 + 1
• 6 + 0

Jedes Ergebnis ergibt jeweils 6.

In welche Zahlen lässt sich die 7 zerlegen?

• 0 + 7
• 1 + 6
• 2 + 5
• 3 + 4
• 4 + 3
• 5 + 2
• 6 + 1
• 7 + 0

Jedes Ergebnis ergibt jeweils 7.

In welche Zahlen lässt sich die 8 zerlegen?

• 0 + 8
• 1 + 7
• 2 + 6
• 3 + 5
• 4 + 4
• 5 + 3
• 6 + 2
• 7 + 1
• 8 + 0

Jedes Ergebnis ergibt jeweils 8.

In welche Zahlen lässt sich die 9 zerlegen?

• 0 + 9
• 1 + 8
• 2 + 7
• 3 + 6
• 4 + 5
• 5 + 4
• 6 + 3
• 7 + 2
• 8 + 1
• 9 + 0

Jedes Ergebnis ergibt jeweils 9.

In welche Zahlen lässt sich die 10 zerlegen?

• 0 + 10
• 1 + 9
• 2 + 8
• 3 + 7
• 4 + 6
• 5 + 5
• 6 + 4
• 7 + 3
• 8 + 2
• 9 + 1
• 10 + 0

Jedes Ergebnis ergibt jeweils 10.

Darstellungsformen für die Zahlzerlegung

Die Zahlzerlegung kann mit Hilfe von Zahlentürmen, Rechentürmen, Rechenhäusern, Zahlenhäusern, Schüttelboxen usw. dargestellt werden.

Einen ausführlichen Beitrag zur Anwendung der Schüttelbox findest du unter Schüttelbox – eine von vielen Möglichkeiten zur Zahlzerlegung.

Auch ein Teller oder Schachteln mit 3 Fächern können zum Üben der Zahlenzerlegung herangezogen werden.

Weitere Beiträge zu anderen Formen der Darstellung werden folgen.

Was sonst noch in der 1.Klasse Mathematik durchgenommen wird kannst du auf der Seite 1. Klasse Mathematik nachlesen.

---

Quelle: Wissen inklusiv

Schlagworte: Zahlzerlegung, Klasse 1. Mathematik, 1.Klasse Mathematik, Mathe 1.Klasse, Klasse 1 Mathematik, Klasse 1 Mathe, Zahlenraum 10, ZR10